专题16 圆锥曲线的标准方程与几何性质（3知识点 2重难点 9方法技巧 3易错易混）（解析版）-2025年高考数学一轮复习知识清单

专题16圆锥曲线的标准方程与几何性质

（思维构建+知识盘点+重点突破+方法技巧+易混易错）

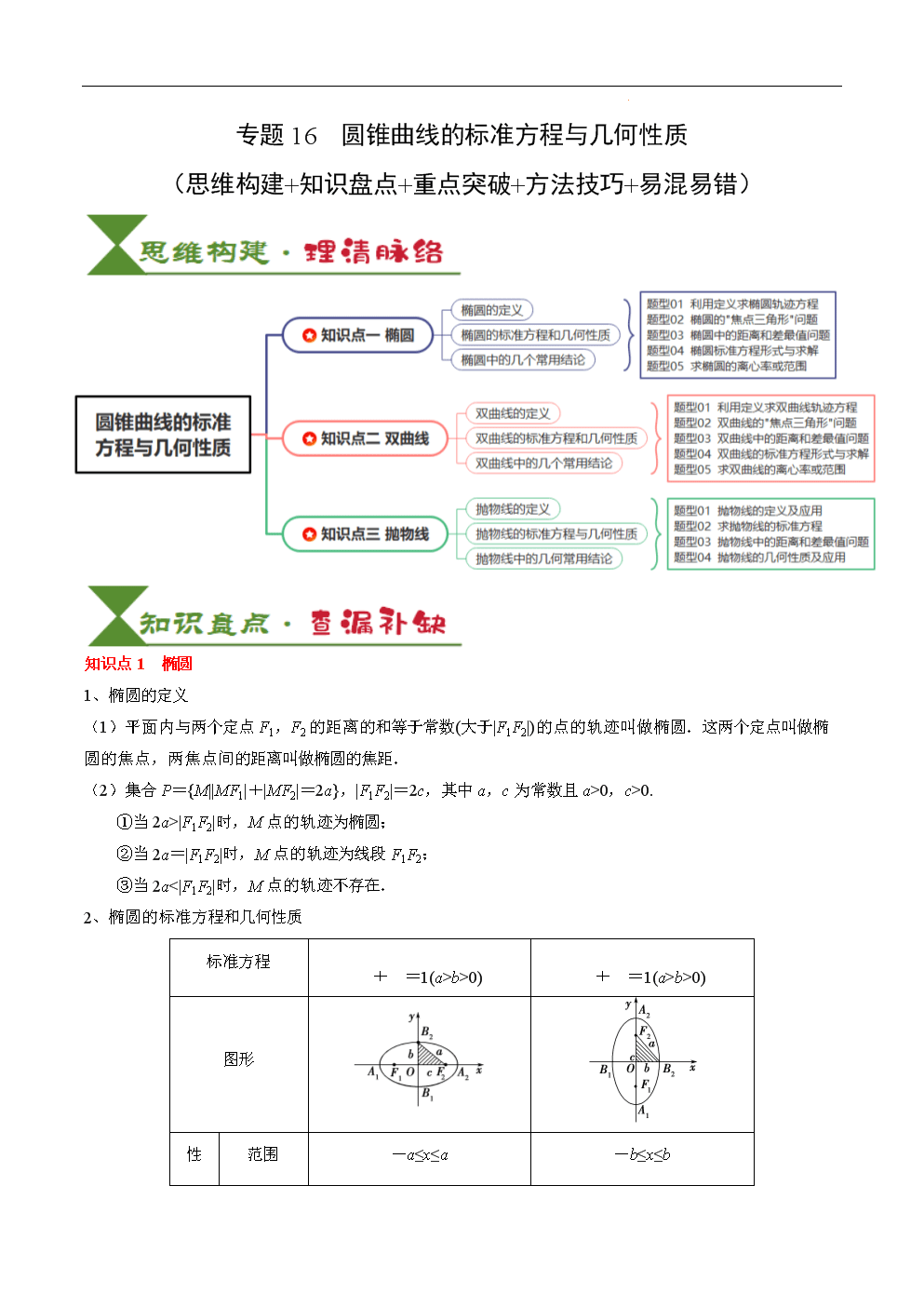
知识点1椭圆

1、椭圆的定义

（1）平面内与两个定点F1，F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆．这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距．

（2）集合P＝{M||MF1|＋|MF2|＝2a}，|F1F2|＝2c，其中a，c为常数且a0，c0.

①当2a|F1F2|时，M点的轨迹为椭圆；

②当2a＝|F1F2|时，M点的轨迹为线段F1F2；

③当2a|F1F2|时，M点的轨迹不存在．

2、椭圆的标准方程和几何性质

标准方程

eq\f(x2,a2)＋eq\f(y2,b2)＝1(ab0)

eq\f(y2,a2)＋eq\f(x2,b2)＝1(ab0)

图形

性

质

范围

－a≤x≤a

－b≤y≤b

－b≤x≤b

－a≤y≤a

对称性

对称轴：坐标轴；对称中心：原点

顶点

A1(－a,0)，A2(a,0)，

B1(0，－b)，B2(0，b)

A1(0，－a)，A2(0，a)，

B1(－b,0)，B2(b,0)

离心率

e＝eq\f(c,a)，且e∈(0,1)

a，b，c的关系

c2＝a2－b2

3、椭圆中的几个常用结论

（1）过椭圆焦点垂直于长轴的弦是最短的弦，长为eq\f(2b2,a)，过焦点最长弦为长轴．

（2）过原点最长弦为长轴长2a，最短弦为短轴长2b.

（3）与椭圆eq\f(x2,a2)＋eq\f(y2,b2)＝1(a＞b＞0)有共同焦点的椭圆方程为eq\f(x2,a2＋λ)＋eq\f(y2,b2＋λ)＝1(λ＞－b2)．

（4）焦点三角形：椭圆上的点P(x0，y0)与两焦点F1，F2构成的△PF1F2叫做焦点三角形．

若r1＝|PF1|，r2＝|PF2|，∠F1PF2＝θ，△PF1F2的面积为S，则在椭圆eq\f(x2,a2)＋eq\f(y2,b2)＝1(a＞b＞0)中：

①当r1＝r2，即点P为短轴端点时，θ最大；

②S＝eq\f(1,2)|PF1||PF2|sinθ＝c|y0|，当|y0|＝b，即点P为短轴端点时，S取得最大值，最大值为bc；

③△PF1F2的周长为2(a＋c)．

知识点2双曲线

1、双曲线的定义

（1）平面内与两个定点F1，F2(|F1F2|＝2c0)的距离之差的绝对值为非零常数2a(2a2c)的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点．

（2）集合P＝{M|||MF1|－|MF2||＝2a}，|F1F2|＝2c，其中a，c为常数且a0，c0.

①当2a|F1F2|时，M点的轨迹是双曲线；

②当2a＝|F1F2|时，M点的轨迹是两条射线；

③当2a|F1F2|时，M点不存在．

2、双曲线的标准方程和几何性质

标准方程

eq\f(x2,a2)－eq\f(y2,b2)＝1(a0，b0)

eq\f(y2,a2)－eq\f(x2,b2)＝1(a0，b0)

图形

性质

范围

x≥a或x≤－a，y∈R

y≤－a或y≥a，x∈R

对称性

对称轴：坐标轴，对称中心：原点

顶点

A1(－a,0)，A2(a,0)

A1(0，－a)，A2(0，a)

渐近线

y＝±eq\f(b,a)x

y＝±eq\f(a,b)x

离心率

e＝eq\f(c,a)，e∈(1，＋∞)

实、虚轴

线段A1A2叫做双曲线的实轴，它的长|A1A2|＝2a；

线段B1B2叫做双曲线的虚轴，它的长|B1B2|＝2b；

a叫做双曲线的实半轴长，b叫做双曲线的虚半轴长

a，b，c的关系

c2＝a2＋b2(ca0，cb0)

3、双曲线中的几个常用结论

（1）双曲线的焦点到其渐近线的距离为b.

（2）若P是双曲线右支上一点，F1，F2分别为双曲线的左、右焦点，则|PF1|min＝a＋c，|PF2|min＝c－a.

（3）同支的焦点弦中最短的为通径(过焦点且垂直于长轴的弦)，其长为eq\f(2b2,a)，异支的弦中最短的为实轴，其长为2a.

（4）设P，A，B是双曲线上的三个不同的点，其中A，B关于原点对称，直线PA，PB斜率存在且不为0，则直线PA与PB的斜率之积为eq\f(b2,a2).

（5）P是双曲线上不同于实轴两端点的任意一点，F1，F2分别为双曲线的左、右焦点，则，其中θ为∠F1PF2.

（6）等轴双曲线

①定义：中心在原点，以坐标轴为对称轴，实半轴长与虚半轴长相等的双曲线叫做等轴双曲线．

②性质：a＝b;e＝eq\r(2)；渐近线互相垂直；等轴双曲线上任意一点到中心的距离是它到两焦点距离的等比中项．

（7）共轭双曲线

①定义：若一条双曲线的实轴和虚轴分别是另一条双曲线的虚轴和实轴，那么这两条双曲线互为共轭双曲线．

②性质：它们有共同的渐近线；它们的四个焦点共圆

免费下载链接
飞猫云链接地址：https://jmj.cc/s/7ir9z1

压缩包解压密码：res.99hah.com_gamWkCmkLz

下载方法：如果您不是飞猫云会员，请在下载页面滚动到最下方，点击“非会员下载”，网页跳转后再次滚动到最下方，点击“非会员下载”。

解压软件：Bandizip